Menguasai cara mengerjakan soal matematika pecahan adalah kunci sukses dalam matematika. Panduan komprehensif ini akan memandu Anda melalui langkah-langkah penting, konsep dasar, dan strategi efektif untuk menaklukkan soal-soal pecahan yang menantang.
Pecahan, dengan penyebut dan pembilangnya, banyak digunakan dalam kehidupan sehari-hari, mulai dari mengukur bahan makanan hingga menghitung diskon. Memahaminya akan membuka pintu ke berbagai bidang.
Menganalisis Soal Matematika Pecahan
Menganalisis soal matematika pecahan adalah langkah penting untuk menyelesaikannya dengan benar. Dengan memahami apa yang ditanyakan soal, kita dapat menentukan strategi terbaik untuk menyelesaikannya.
Berikut langkah-langkah menganalisis soal matematika pecahan:
- Baca soal dengan cermat dan identifikasi informasi yang diberikan.
- Tentukan operasi matematika yang digunakan (misalnya penjumlahan, pengurangan, perkalian, pembagian).
- Identifikasi pecahan yang terlibat dan ubah ke bentuk yang lebih sederhana jika memungkinkan.
- Buat rencana langkah demi langkah untuk menyelesaikan soal.
Contoh Soal
Sebuah toko roti memiliki 3/4 loyang adonan kue. Toko tersebut menggunakan 1/2 loyang adonan untuk membuat kue. Berapa loyang adonan kue yang tersisa?
Analisis Soal
- Operasi matematika yang digunakan: Pengurangan
- Pecahan yang terlibat: 3/4 dan 1/2
- Bentuk yang lebih sederhana: Tidak perlu
- Rencana langkah demi langkah: Kurangi 1/2 dari 3/4
Memahami Konsep Pecahan
Pecahan adalah cara untuk mewakili bagian dari keseluruhan. Pecahan terdiri dari dua bagian utama: pembilang dan penyebut.
Pembilang dan Penyebut
Pembilang adalah angka di atas garis pecahan, yang menunjukkan jumlah bagian yang diambil. Penyebut adalah angka di bawah garis pecahan, yang menunjukkan jumlah total bagian dalam keseluruhan.
Bentuk Desimal
Pecahan juga dapat ditulis dalam bentuk desimal. Bentuk desimal adalah representasi pecahan sebagai angka yang setara dalam bentuk desimal. Untuk mengubah pecahan menjadi desimal, kita membagi pembilang dengan penyebut.
Dalam mengerjakan soal matematika pecahan, pemahaman konsep dasar sangat penting. Setelah menguasai konsepnya, langkah berikutnya adalah mengetahui cara menjawab soal dengan tepat. Untuk mempelajari teknik menjawab soal secara efektif, kamu bisa merujuk pada cara menjawab soal. Dengan memahami teknik tersebut, kamu dapat mengidentifikasi tipe soal, menyusun strategi pengerjaan, dan mengeksekusinya dengan benar.
Pemahaman cara menjawab soal yang baik akan sangat membantu dalam menyelesaikan soal matematika pecahan secara efektif dan akurat.
Contoh Penggunaan Pecahan dalam Kehidupan Sehari-hari
- Membagi pizza: Jika sebuah pizza dibagi menjadi 8 bagian dan Anda mengambil 3 bagian, maka bagian yang Anda ambil dapat dinyatakan sebagai pecahan 3/8.
- Mengukur waktu: Satu jam memiliki 60 menit. Jika Anda telah bekerja selama 30 menit, maka waktu yang telah Anda kerjakan dapat dinyatakan sebagai pecahan 30/60 atau 0,5 (dalam bentuk desimal).
- Memasak: Dalam resep, bahan-bahan sering kali dinyatakan dalam bentuk pecahan. Misalnya, resep mungkin memerlukan 1/2 cangkir tepung.
Operasi Hitung Pecahan
Dalam matematika, pecahan adalah bilangan yang menyatakan bagian dari keseluruhan. Pecahan terdiri dari pembilang (angka di atas) dan penyebut (angka di bawah). Operasi hitung dasar untuk pecahan meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
Penjumlahan dan Pengurangan Pecahan
Untuk menjumlahkan atau mengurangkan pecahan dengan penyebut yang sama, cukup jumlahkan atau kurangkan pembilangnya, dan pertahankan penyebutnya. Jika penyebutnya berbeda, kita harus mencari penyebut persekutuan terkecil (FPB) terlebih dahulu. Setelah mendapatkan FPB, ubah kedua pecahan menjadi pecahan ekuivalen dengan penyebut FPB, lalu jumlahkan atau kurangkan pembilangnya.
- Contoh: Menjumlahkan 1/2 dan 1/3
- FPB dari 2 dan 3 adalah 6
- Ubah 1/2 menjadi 3/6 dan 1/3 menjadi 2/6
- 3/6 + 2/6 = 5/6
Perkalian Pecahan
Untuk mengalikan dua pecahan, cukup kalikan pembilang dengan pembilang dan penyebut dengan penyebut.
- Contoh: Mengalikan 1/2 dengan 2/3
- 1/2 x 2/3 = (1 x 2) / (2 x 3) = 2/6 = 1/3
Pembagian Pecahan, Cara mengerjakan soal matematika pecahan
Untuk membagi pecahan, cukup balik pecahan kedua (pembagi) dan kemudian kalikan. Ingat, pembilang menjadi penyebut dan penyebut menjadi pembilang.
- Contoh: Membagi 1/2 dengan 1/3
- 1/2 ÷ 1/3 = 1/2 x 3/1 = 3/2
Strategi Mengerjakan Soal Pecahan
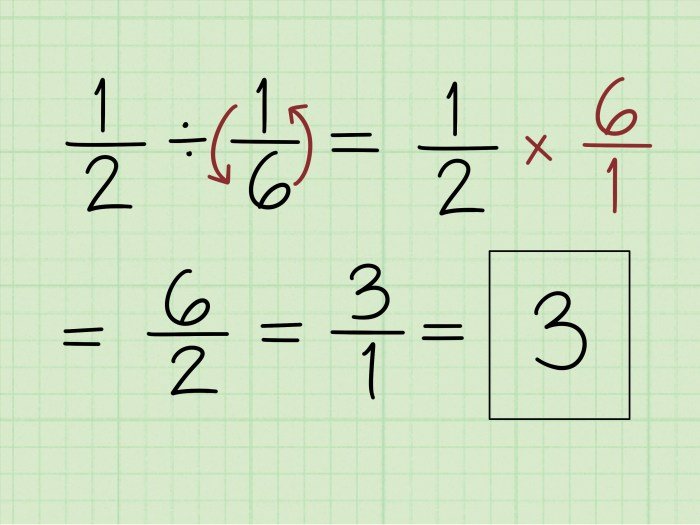
Mengerjakan soal matematika pecahan memerlukan strategi efektif. Dengan memahami strategi ini, Anda dapat memecahkan soal dengan lebih efisien dan akurat.
Menyederhanakan Pecahan
Sebelum mengerjakan soal, sederhanakan pecahan ke bentuk paling sederhana. Ini dilakukan dengan mencari faktor persekutuan terbesar (FPB) dari pembilang dan penyebut dan membagi keduanya dengan FPB tersebut.
Contoh:Sederhanakan pecahan 12/18.
- FPB dari 12 dan 18 adalah 6.
- Membagi pembilang dan penyebut dengan 6 menghasilkan pecahan sederhana 2/3.
Mengubah ke Bentuk Desimal
Jika memungkinkan, ubah pecahan ke bentuk desimal. Ini memudahkan perhitungan, terutama jika pecahan melibatkan angka desimal.
Contoh:Ubah pecahan 3/4 ke bentuk desimal.
- Membagi 3 dengan 4 menggunakan kalkulator atau pembagian panjang menghasilkan desimal 0,75.
Menggunakan Gambar atau Diagram
Untuk soal pecahan yang kompleks, menggunakan gambar atau diagram dapat membantu memvisualisasikan masalah dan menemukan solusi.
Contoh:Soal: Sebuah pizza dibagi menjadi 8 bagian yang sama. Jika Adi memakan 3/8 pizza, berapa bagian pizza yang tersisa?
- Menggambar pizza yang dibagi menjadi 8 bagian.
- Menarsir 3 bagian untuk menunjukkan bagian yang dimakan Adi.
- Bagian yang tersisa adalah 8 bagian dikurangi 3 bagian, yaitu 5 bagian.
Soal Cerita Pecahan
Soal cerita pecahan menguji kemampuan Anda dalam memahami dan menerapkan konsep pecahan dalam situasi dunia nyata.
Mengerjakan soal matematika pecahan membutuhkan ketelitian dan pemahaman konsep. Sama seperti saat mengerjakan shalat sunnah rawatib, yang juga memerlukan perhatian dan niat yang benar ( bagaimana cara mengerjakan shalat sunnah rawatib ). Kembali ke soal pecahan, penting untuk memahami konsep pecahan dan operasi matematika yang terkait, seperti penjumlahan, pengurangan, dan pembagian.
Cara Memahami dan Menyelesaikan Soal Cerita Pecahan
Untuk menyelesaikan soal cerita pecahan, ikuti langkah-langkah berikut:
- Baca soal dengan cermat dan identifikasi informasi penting, seperti jumlah, pecahan, dan hubungan di antara mereka.
- Terjemahkan informasi ke dalam bentuk matematika. Misalnya, jika soal menyatakan “setengah dari apel”, tulislah sebagai 1/2 x jumlah apel.
- Sederhanakan persamaan matematika dan selesaikan untuk variabel yang tidak diketahui.
- Periksa jawaban Anda untuk memastikan bahwa jawaban tersebut masuk akal dan memenuhi kondisi soal.
Contoh Soal Cerita Pecahan
Andi memiliki 12 apel. Dia memberikan setengahnya kepada temannya. Berapa jumlah apel yang diberikan Andi kepada temannya?
Dalam mengerjakan soal matematika pecahan, kita perlu memahami konsep kesetaraan pecahan. Sama seperti dalam sholat qobliyah subuh, di mana kita mengawali dengan membaca niat yang menjadi dasar kesahan sholat ( cara mengerjakan sholat qobliyah subuh ). Dengan memahami kesetaraan pecahan, kita dapat menyelesaikan soal matematika pecahan dengan lebih mudah.
Kesetaraan pecahan juga membantu kita dalam kehidupan sehari-hari, seperti saat membagi kue secara adil atau mengonversi satuan ukuran.
Langkah-langkah Penyelesaian:
- Informasi penting: Andi memiliki 12 apel, dan dia memberikan setengahnya.
- Persamaan matematika: 1/2 x 12 = jumlah apel yang diberikan
- Penyederhanaan: 6 = jumlah apel yang diberikan
- Jawaban: Andi memberikan 6 apel kepada temannya.
Tips dan Latihan
Kemahiran dalam mengerjakan soal matematika pecahan merupakan landasan penting dalam matematika. Berikut beberapa tips dan latihan untuk membantu Anda mempersiapkan diri menghadapi soal-soal pecahan:
Memahami konsep dasar pecahan sangat penting. Pastikan Anda memahami cara membandingkan, menambah, mengurangkan, mengalikan, dan membagi pecahan.
Latihan secara teratur sangat penting untuk meningkatkan keterampilan Anda. Berlatihlah mengerjakan berbagai jenis soal pecahan, termasuk yang melibatkan pecahan campuran dan desimal.
- Berlatihlah mengubah pecahan ke bentuk desimal dan sebaliknya.
- Pelajari cara menyederhanakan pecahan ke bentuk paling sederhana.
- Kuasai operasi matematika dasar (penjumlahan, pengurangan, perkalian, dan pembagian) pada pecahan.
- Berlatihlah menyelesaikan soal cerita yang melibatkan pecahan.
Dengan mengikuti tips ini dan mengerjakan latihan secara teratur, Anda dapat meningkatkan keterampilan matematika pecahan Anda secara signifikan.
| Tingkat Kesulitan | Contoh Soal |
|---|---|
| Mudah | Sederhanakan pecahan 6/12 |
| Sedang | Tambahkan pecahan 1/2 dan 1/4 |
| Sulit | Kalikan pecahan 3/4 dengan 2/5 |
“Pemahaman matematika pecahan sangat penting untuk kesuksesan di bidang sains, teknologi, teknik, dan matematika (STEM).”
Kesimpulan Akhir
Dengan menguasai konsep dan teknik yang diuraikan dalam panduan ini, Anda akan memiliki kepercayaan diri dan kemampuan untuk mengatasi soal matematika pecahan dengan mudah. Ingatlah, latihan teratur dan pemahaman mendasar adalah kunci sukses. Selamat menjelajah dunia pecahan!
Ringkasan FAQ: Cara Mengerjakan Soal Matematika Pecahan
Apa yang dimaksud dengan pecahan?
Pecahan adalah bagian dari keseluruhan yang dibagi menjadi bagian-bagian yang sama.
Bagaimana cara menyederhanakan pecahan?
Bagi penyebut dan pembilang dengan faktor persekutuan terbesar (FPB).
Apa strategi efektif untuk mengerjakan soal cerita pecahan?
Baca soal dengan cermat, identifikasi informasi penting, dan buatlah model matematika untuk menyelesaikannya.
