Menguasai cara mengerjakan akar kuadrat membuka gerbang menuju dunia matematika yang lebih kompleks. Akar kuadrat, simbol matematika yang mewakili kuantitas yang dikalikan dengan dirinya sendiri, adalah kunci untuk memahami konsep aljabar dan kalkulus yang lebih tinggi.
Artikel komprehensif ini akan memandu Anda melalui seluk-beluk akar kuadrat, menjelaskan konsep dasar, metode pemecahan, strategi pengerjaan soal, dan sumber belajar untuk memperkuat pemahaman Anda.
Memahami Konsep Akar Kuadrat

Akar kuadrat adalah bilangan yang, jika dikuadratkan (dikalikan dengan dirinya sendiri), menghasilkan bilangan asli yang diberikan. Simbol untuk akar kuadrat adalah √, dan terbaca sebagai “akar dari”.
Mengerjakan akar kuadrat memang memerlukan pemahaman konsep yang jelas. Nah, sama halnya saat menjawab panggilan interview. Penting untuk mengetahui teknik dan tips agar dapat menjawab pertanyaan dengan baik dan meyakinkan. Anda dapat mencari informasi mengenai cara menjawab panggilan interview secara lebih mendalam di internet.
Kembali ke topik akar kuadrat, selalu ingat untuk memeriksa kembali jawaban Anda untuk memastikan akurasi.
Contoh bilangan yang memiliki akar kuadrat meliputi 4, 9, 16, 25, dan seterusnya. Akar kuadrat dari bilangan-bilangan ini masing-masing adalah 2, 3, 4, 5, dan seterusnya.
Sifat-sifat Akar Kuadrat
- Akar kuadrat dari bilangan positif selalu positif.
- Akar kuadrat dari 0 adalah 0.
- Akar kuadrat dari bilangan negatif tidak nyata (imajiner).
- Akar kuadrat dari perkalian dua bilangan positif sama dengan perkalian akar kuadrat masing-masing bilangan.
- Akar kuadrat dari pembagian dua bilangan positif sama dengan pembagian akar kuadrat masing-masing bilangan.
Metode Mencari Akar Kuadrat: Cara Mengerjakan Akar Kuadrat
Mencari akar kuadrat suatu bilangan adalah proses menemukan bilangan yang jika dikuadratkan menghasilkan bilangan asli yang diberikan. Ada beberapa metode untuk mencari akar kuadrat, salah satunya adalah faktorisasi prima.
Faktorisasi Prima, Cara mengerjakan akar kuadrat
Faktorisasi prima adalah proses mengurai suatu bilangan menjadi faktor-faktor primanya. Faktor prima adalah bilangan prima yang membagi habis bilangan yang diberikan.
- Langkah-langkah:
- Bagilah bilangan dengan bilangan prima terkecil yang membagi habisnya.
- Ulangi langkah 1 sampai bilangan tidak dapat dibagi lagi dengan bilangan prima.
- Faktor-faktor prima adalah bilangan prima yang diperoleh dari pembagian.
Tabel Proses Faktorisasi Prima:
| Bilangan | Pembagi Prima | Hasil |
|---|---|---|
| 121 | 11 | 11 |
| 11 | 11 | 1 |
Contoh:
Carilah akar kuadrat dari 121 menggunakan faktorisasi prima:
- 121 = 11 x 11
- Akar kuadrat dari 121 adalah √(11 x 11) = √11 x √11 = 11
Menggunakan Kalkulator
Selain faktorisasi prima, Anda juga dapat menggunakan kalkulator untuk mencari akar kuadrat. Kebanyakan kalkulator memiliki tombol akar kuadrat (√). Untuk mencari akar kuadrat suatu bilangan, cukup masukkan bilangan tersebut ke kalkulator dan tekan tombol akar kuadrat.
Strategi Mengerjakan Soal Akar Kuadrat

Mengerjakan soal akar kuadrat dapat menjadi tugas yang menantang, tetapi dengan strategi yang tepat, kamu dapat menaklukkannya dengan mudah. Berikut adalah beberapa strategi untuk membantumu mengatasi soal-soal akar kuadrat:
Mengidentifikasi Jenis Soal
Sebelum mulai mengerjakan soal, penting untuk mengidentifikasi jenis soal akar kuadrat yang dihadapi. Jenis soal yang umum meliputi:
- Mencari nilai akar kuadrat dari suatu bilangan
- Menyederhanakan ekspresi akar kuadrat
- Memecahkan persamaan akar kuadrat
Manajemen Waktu
Soal akar kuadrat biasanya membutuhkan waktu untuk diselesaikan. Berikut adalah beberapa tips untuk mengelola waktu secara efektif:
- Baca soal dengan cermat dan pahami apa yang ditanyakan.
- Identifikasi langkah-langkah yang diperlukan untuk menyelesaikan soal.
- Bagi waktu secara proporsional untuk setiap langkah.
- Jangan terjebak pada satu langkah terlalu lama.
Teknik Eliminasi Pilihan
Untuk soal pilihan ganda, teknik eliminasi pilihan dapat membantu mempersempit pilihan dan meningkatkan peluang untuk menjawab dengan benar:
- Hilangkan pilihan yang jelas-jelas salah.
- Bandingkan pilihan yang tersisa dan cari kesamaan atau perbedaan.
- Periksa pilihan yang tersisa dengan hati-hati untuk memastikan kebenarannya.
4. Latihan dan Penguatan

Untuk memperkuat pemahaman tentang akar kuadrat, latihan dan penguatan sangat penting. Ini dapat dicapai melalui berbagai cara.
Menemukan akar kuadrat dapat dilakukan dengan beberapa metode, seperti pemfaktoran atau pembagian panjang. Untuk pemfaktoran, cari dua faktor yang jika dikalikan hasilnya sama dengan bilangan yang ingin dicari akarnya. Sebaliknya, jika ingin mengasah spiritualitas, dianjurkan untuk mempelajari cara mengerjakan sholat tahajud.
Sholat tahajud merupakan ibadah sunnah yang dikerjakan pada sepertiga malam terakhir. Kembali ke akar kuadrat, pembagian panjang juga bisa digunakan dengan membagi bilangan tersebut dengan bilangan yang lebih kecil dari akar kuadratnya.
Salah satu cara yang efektif adalah merancang latihan soal akar kuadrat dengan tingkat kesulitan yang bervariasi. Latihan soal ini dapat mencakup soal-soal sederhana hingga kompleks, sehingga siswa dapat menguji pemahaman mereka secara bertahap.
Simulasi Ujian
Simulasi ujian juga dapat bermanfaat untuk mempersiapkan siswa menghadapi ujian sebenarnya. Simulasi ini dapat mencakup soal-soal akar kuadrat dengan format dan tingkat kesulitan yang mirip dengan ujian.
Dalam mengerjakan akar kuadrat, kita dapat menggunakan berbagai metode seperti pengambilan faktor prima atau cara panjang. Setelah menguasai cara mengerjakan akar kuadrat, tidak ada salahnya kita mempelajari hal lain yang juga bermanfaat, seperti cara menjawab adzan. Dengan mengetahui cara menjawab adzan, kita dapat merespons panggilan ibadah dengan baik dan benar.
Setelah mempelajari cara menjawab adzan, kita dapat kembali mengasah keterampilan mengerjakan akar kuadrat untuk menyelesaikan soal-soal matematika dengan lebih efisien.
Belajar Kelompok
Belajar kelompok dapat menjadi cara yang efektif untuk memperkuat pemahaman tentang akar kuadrat. Siswa dapat bekerja sama untuk menyelesaikan soal, mendiskusikan konsep, dan memberikan penjelasan kepada teman sekelas mereka.
Dengan berpartisipasi dalam diskusi kelompok, siswa dapat memperoleh perspektif yang berbeda, mengidentifikasi kesenjangan dalam pemahaman mereka, dan meningkatkan keterampilan pemecahan masalah mereka.
Sumber Belajar dan Bantuan
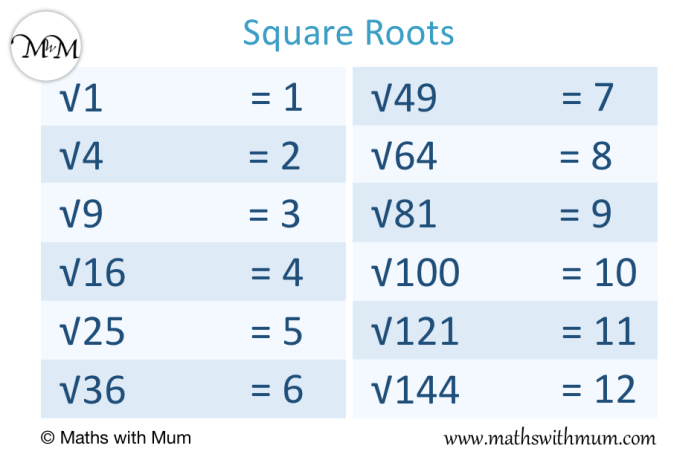
Perluas pemahaman Anda tentang akar kuadrat dengan memanfaatkan berbagai sumber belajar yang tersedia.
Sumber-sumber ini dapat membantu Anda memahami konsep dasar, berlatih soal, dan mendapatkan bantuan dari para ahli.
Sumber Belajar Online
- Khan Academy: Platform pembelajaran online yang menawarkan video, latihan interaktif, dan kuis.
- Brilliant: Platform pembelajaran interaktif dengan pelajaran akar kuadrat yang komprehensif.
- Mathway: Aplikasi dan situs web yang menyediakan solusi langkah demi langkah untuk soal akar kuadrat.
- Varsity Tutors: Platform bimbingan belajar online yang menawarkan tutor berpengalaman untuk akar kuadrat.
Sumber Belajar Offline
- Buku Teks: Buku teks matematika biasanya memiliki bab yang didedikasikan untuk akar kuadrat.
- Buku Kerja: Buku kerja khusus akar kuadrat menyediakan banyak latihan dan soal.
- Perpustakaan: Perpustakaan lokal sering kali memiliki buku dan sumber daya tentang akar kuadrat.
Bantuan Guru dan Tutor
Jangan ragu untuk mencari bantuan dari guru atau tutor jika Anda mengalami kesulitan memahami akar kuadrat.
- Guru Matematika: Guru matematika Anda dapat memberikan penjelasan tambahan, contoh, dan latihan.
- Tutor: Tutor yang berpengalaman dapat memberikan bimbingan khusus dan membantu Anda menguasai akar kuadrat.
Mencatat dan Ringkasan
Mencatat rumus dan membuat ringkasan dapat sangat membantu dalam memahami dan mengingat konsep akar kuadrat.
- Rumus Akar Kuadrat: $\sqrta = b$, di mana $b^2 = a$
- Contoh Ringkasan:
- Definisi akar kuadrat
- Rumus untuk menghitung akar kuadrat
- Aplikasi akar kuadrat dalam kehidupan nyata
Visualisasi dan Representasi
Memvisualisasikan konsep akar kuadrat dapat membantu meningkatkan pemahaman dan retensi. Berikut beberapa cara untuk menggambarkan dan merepresentasikan akar kuadrat:
Diagram Ilustratif
Gambarlah persegi dengan sisi yang sama dengan bilangan yang ingin Anda cari akar kuadratnya. Misalnya, untuk mencari akar kuadrat dari 16, gambarlah persegi dengan sisi 4. Akar kuadrat dari 16 adalah panjang diagonal persegi tersebut.
Tabel Perbandingan Metode
| Metode | Keuntungan | Kelemahan |
|---|---|---|
| Pemfaktoran Prima | Sederhana untuk bilangan yang dapat difaktorkan | Sulit untuk bilangan yang besar atau tidak dapat difaktorkan |
| Metode Newton-Raphson | Iteratif dan dapat menemukan akar kuadrat dari bilangan apa pun | Membutuhkan perkiraan awal yang baik |
| Algoritma Babylonian | Iteratif dan biasanya konvergen dengan cepat | Tidak cocok untuk bilangan yang sangat kecil |
Mind Mapping
Buatlah peta konsep untuk memetakan hubungan antara konsep akar kuadrat. Sertakan konsep seperti kuadrat, akar, diagonal, persegi, dan metode penghitungan.
Ringkasan Akhir
Dengan menguasai cara mengerjakan akar kuadrat, Anda akan membuka pintu menuju pemahaman yang lebih dalam tentang matematika dan meningkatkan kemampuan pemecahan masalah Anda secara signifikan. Jadi, mari selami dunia akar kuadrat dan taklukkan tantangan matematika yang ada di depan Anda!
Pertanyaan Populer dan Jawabannya
Apa itu akar kuadrat?
Akar kuadrat suatu bilangan adalah bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan tersebut.
Bagaimana cara mencari akar kuadrat menggunakan kalkulator?
Masuk angka ke kalkulator dan tekan tombol “√” atau “sqr”.
Apa manfaat belajar akar kuadrat?
Mengerjakan akar kuadrat memperkuat keterampilan aljabar, meningkatkan pemecahan masalah, dan membuka pemahaman konsep matematika yang lebih tinggi.
